I came across the fact that a random walk on an infinite 2d grid almost surely returns to the origin, and thought the proof was pretty cool.

Precise Statement: Suppose you start at $(0,0)$. Every minute, you take one step in the $+x$, $-x$, $+y$, or $-y$ directions, each with probability $\frac14$. You'll almost surely return back to $(0,0)$ at some point in the future.

First, let

$$F(x) = \sum_{t=1}^\infty f_tx^t$$

be the infinite series where $f_t$ gives the probability of returning to the origin for the FIRST time on the $t$th step of the walk. (The first few terms of $F(x)$ are $\frac14x^2 + \frac{5}{64}x^4 + \frac{11}{256}x^6 + \cdots$).

Also, let

$$R(x) = \sum_{t=1}^\infty r_tx^t$$

be a similar series, only that $r_t$ includes REPEATED visits to the origin as well. (Its first few terms are $\frac14x^2 + \frac{9}{64}x^4 + \frac{25}{256}x^6 + \cdots$).

Now $F$ and $R$ are related, in that any walk that visits the origin multiple times can be decomposed into smaller segments for every time it visits the origin. For example, the product $F(x) \cdot F(x)$ represents a generating function for the probability of being at the origin for the $2$nd time. It sums terms $f_xf_y$ over all $x+y=t$, representing the walks that first return to the origin on step $x$ and then again on step $x+y$.

Similarly, $F(x)^3$ is a generating function for the probability of being at the origin for the $3$rd time, and in general, $F(x)^k$ represents the generating function for being at the origin for the $k$th time. Thus, the probability of being at the origin at any time satisfies

$$R(x) = \sum_{k=1}^\infty F(x)^k = F(x) + F(x)^2 + F(x)^3 + \cdots = \frac{F(x)}{1-F(x)}.$$

Rearranging, this gives

$$F(x) = \frac{R(x)}{R(x)+1}.$$

The ultimate goal is to show that the walk almost surely returns to the origin, or in more precise terms,

$$f_1 + f_2 + f_3 + \cdots = 1.$$

This is equivalent to evaluating $F(1)$, since $1^t = 1$ for all $t$. But from the above relation, we have $F(1) = 1 - \frac{1}{R(1) + 1}$, so it is enough to show that $R(1) = \infty$ diverges.

Claim: $R(1)$ diverges

The idea is that $r_t$ is much easier to compute than $f_t$, since there is no longer a restriction on the prior steps of the walk.

Let $t = 2n$ (since any return to the origin must be at an even time); then $r_{2n}$ is the number of walks returning to the origin, divided by $4^{2n}$ total possible walks. Surprisingly, it's possible to compute this quantity exactly!

Instead of having four possible equally likely movements, look at each movement as two independent choices on whether to increase/decrease $x+y$, and whether to increase/decrease $x-y$:

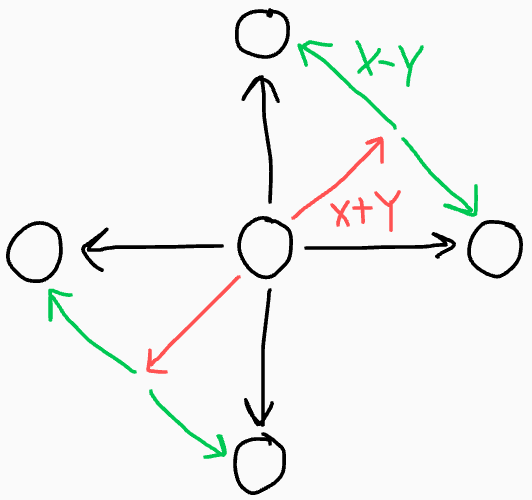
After $2n$ movements, we've made $2n$ red choices and $2n$ green choices. Since the origin has $x+y = 0$, exactly half of the red choices are up-right, and the other half down-left. These can occur in any order, giving $\binom{2n}{n}$ possibilities. Similarly, since the origin has $x-y=0$, there are $\binom{2n}{n}$ ways to arrange the green choices.

Therefore, the total number of walks that return to the origin after $2n$ steps is $\binom{2n}{n}^2$, so

$$r_{2n} = \frac{\binom{2n}{n}^2}{4^{2n}}.$$

By Stirling's approximation, $\binom{2n}{n} \approx \frac{4^n}{\sqrt{\pi n}}$, which gives

$$r_{2n} = \frac{\binom{2n}{n}^2}{4^{2n}} \approx \frac{4^{2n}}{4^{2n}\cdot \pi n} = O(1/n).$$

Since $R(1) = r_2 + r_4 + r_6 + \cdots$ is now bounded by a harmonic series, it diverges, finishing the proof.

What is interesting to note is that in 3D, while the probability of $r_{2n}$ is not easy to determine, it's asymptotic to $O(1/n^{1.5})$ instead of $O(1/n)$. So in 3D, the sum $R(1)$ actually converges, meaning $F(1) < 1$. Empirically, the probability of returning to the origin in 3D is close to $34\%$.