Problem 1: A diagonal is drawn on a $10\times 7$ grid of unit squares, cutting a few of them into triangles, trapezoids, and pentagons. What is the total area of the pentagons?

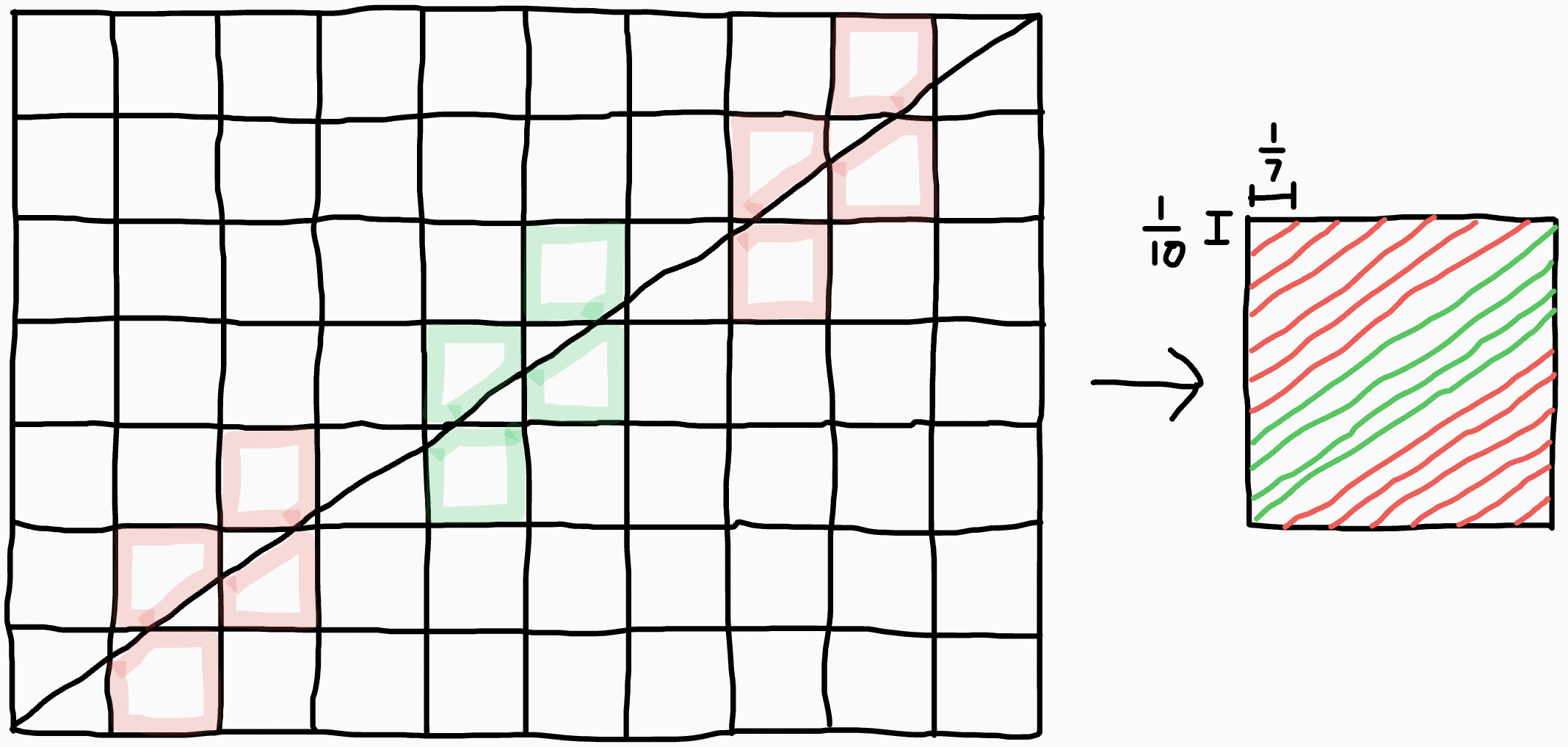
The idea is to translate all the cells into one. In this case, the slice is like shooting a beam of light at a slope of $\frac{7}{10}$ and "wrapping arround" every time the wall of the square is hit. The result is a bunch of equally spaced parallel lines of slope $\frac7{10}$. The squares that are ultimately split into pentagons are the red lines in the picture.

The pentagon areas can be found by adding the areas of the highlighted squares, and subtracting the triangular regions. Since the triangles are all similar to each other, we can take the smallest triangle's area, and add up all the other scale factors:

The answer happens to be $10.7$, the concatenation of the only two numbers in the problem.

Problem 2: Let $m$ and $n$ be positive integers. In terms of $m$ and $n$, how many up-right paths on a $2m\times 2n$ grid cut it into two domino-tileable regions?

It can be shown that valid cuts come from alternating the moves of any two paths on an $m\times n$ grid. For instance, when $(m,n) = (2,3)$, the paths $\texttt{RURRU}$ and $\texttt{RRUUR}$ combine to make the cut $\texttt{RR-UR-RU-RU-UR}$:

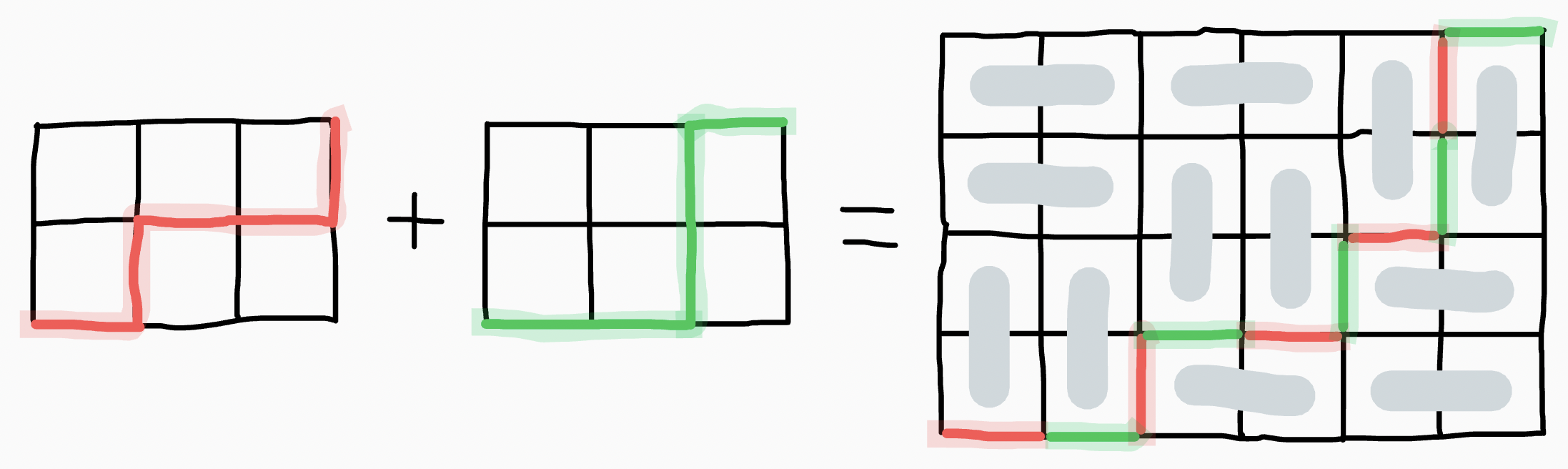
This means the answer is $\binom{n+m}{n}^2 - 2$, since there are two paths along the edge of the grid that don't actually cut the grid.